1.(25分)考虑下面的线性规划问题:
max Z=cTx
s.t. Ax≤b,
x≥0,
其中c=(c1,c2,…,cn)T表示目标函数系数,x=(x1,x2,…,xn)T表示决策变量向量,A是m×n的矩阵,b=(b1,b2,…,bm)T表示右端项。证明最优解构成的集合是凸集。
2.(25分)某城市有8个区,救护车由一个区开到另一个区所需的时间(分钟)如下表所示:
区号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
1 | 0 | 2 | 4 | 6 | 8 | 9 | 8 | 10 |
2 | 0 | 5 | 4 | 8 | 6 | 12 | 9 | |
3 | 0 | 2 | 2 | 3 | 5 | 7 | ||
4 | 0 | 3 | 2 | 5 | 4 | |||
5 | 0 | 2 | 2 | 4 | ||||
6 | 0 | 3 | 2 | |||||
7 | 0 | 2 | ||||||
8 | 0 | |||||||
人口(万人) | P1 | P2 | P3 | P4 | P5 | P6 | P7 | P8 |
其中,P1,P2,...,P8是已知常数。假设从一个区到另一个区的往、返时间相同。该城市只有2辆救护车,市政部门的目标是,希望救护车所在的位置能使尽可能多的人位于救护车在2分钟内可到达的范围内。试帮助市政部门建立合适的整数规划模型,确定救护车停放的最佳区号(只需建立模型,无需求解)。
3.确定以下线性规划问题的所有基本可行解(提示:可借助图解法):(25分)
max Z=x1+x2
s.t. x1+x2≤6,
x1,x2≥0,
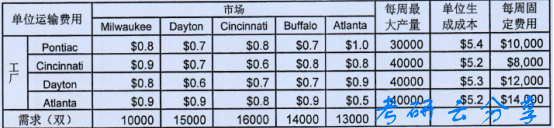
4.(25分)马丁贝克公司是一家中档鞋生产公司。产品主要销往Milwaukee、Dayton、Cincinnati、Buffalo以及Atlanta五个地方,每司的需求分别是10000、15000、16000、14000、13000双。公司决定在Pontiac、Cincinnati、Dayton和Atlanta这四个地方新建一个或几个工厂,以满足市场需求。通过调研,这四个地方各有利弊,例如,Atlanta的生产成本比较低,但运输费用相对较高,具体数据如下表所示。试帮公司确定新工厂的最佳选址,使总成本(包括生产成本、运输成本和固定成本)最低。写出该决策问题的线性规划模型(无需求解)。
5.(25分)写出下面问题的对偶问题:
max 4x1+3x2-x3
subject to x1-x2+x3≥1
x1+2x2-3x3≤2
-5x1+8x3=5
x1≥0,x2≥0,x3无拘束
6.(25分)用割平面法解下面整数规划问题:
min x1-x2
subject to x1+x2≤10
-x1+x2≤5
x1x2≥0,且为整数
